Tìm ảnh của đường tròn qua phép tịnh tiến là một bài toán hình học thú vị, đòi hỏi sự kết hợp giữa tư duy hình học và đại số. Việc nắm vững phương pháp giải bài toán này không chỉ giúp bạn đạt điểm cao trong các kỳ thi mà còn rèn luyện khả năng tư duy logic và phân tích vấn đề. Sau đoạn mở đầu này, chúng ta sẽ cùng nhau đi sâu vào tìm hiểu chi tiết về phép tịnh tiến và ứng dụng của nó trong việc tìm ảnh của đường tròn. Bạn sẽ thấy việc xem vtv6 online nhanh nhất cũng thú vị không kém việc giải quyết vấn đề toán học này.
Phép Tịnh Tiến và Tính Chất Của Nó
Phép tịnh tiến là một phép biến hình bảo toàn khoảng cách giữa các điểm. Nó được xác định bởi một vectơ, gọi là vectơ tịnh tiến. Khi áp dụng phép tịnh tiến lên một hình, mỗi điểm của hình sẽ được di chuyển theo cùng một vectơ tịnh tiến.
Tính Chất Quan Trọng Của Phép Tịnh Tiến
- Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
- Biến đoạn thẳng thành đoạn thẳng bằng nó.
- Biến tam giác thành tam giác bằng nó.
- Biến đường tròn thành đường tròn có cùng bán kính.
Tìm Ảnh Của Đường Tròn Qua Phép Tịnh Tiến: Phương Pháp Đại Số
Phương pháp đại số là một trong những cách tiếp cận hiệu quả để tìm ảnh của đường tròn qua phép tịnh tiến. Bằng cách sử dụng phương trình đường tròn và vectơ tịnh tiến, ta có thể xác định phương trình của đường tròn ảnh.
-
Xác định phương trình đường tròn ban đầu: Giả sử đường tròn (C) có tâm I(a, b) và bán kính R. Phương trình của (C) là (x – a)² + (y – b)² = R².
-
Xác định vectơ tịnh tiến: Vectơ tịnh tiến được ký hiệu là v(x₀, y₀).
-
Tìm tâm I’ của đường tròn ảnh: Tâm I’ của đường tròn ảnh (C’) là ảnh của tâm I qua phép tịnh tiến theo vectơ v. Tọa độ của I’ được tính như sau: I'(a + x₀, b + y₀).
-
Xác định phương trình đường tròn ảnh: Đường tròn ảnh (C’) có tâm I'(a + x₀, b + y₀) và bán kính R (giống đường tròn ban đầu). Phương trình của (C’) là (x – (a + x₀))² + (y – (b + y₀))² = R².
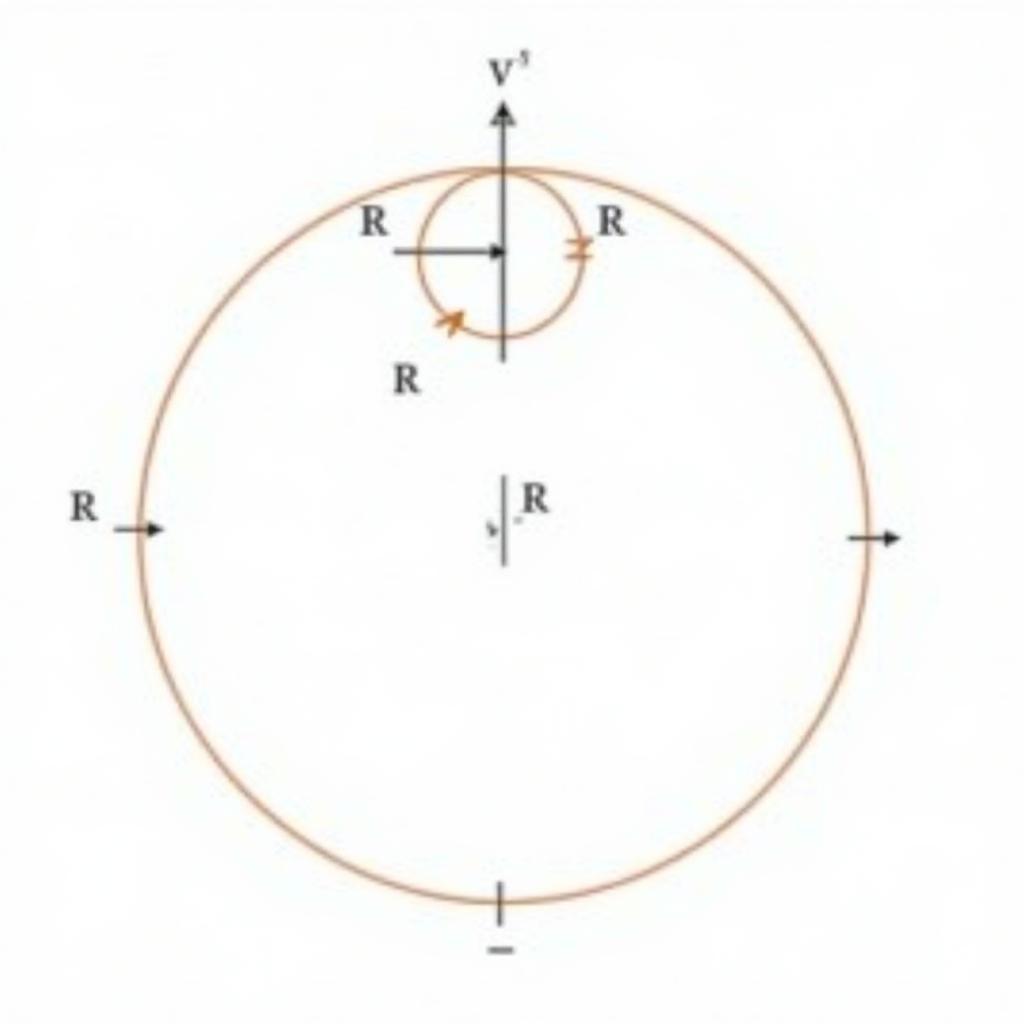 Minh họa phương pháp đại số tìm ảnh đường tròn qua phép tịnh tiến
Minh họa phương pháp đại số tìm ảnh đường tròn qua phép tịnh tiến
Tìm Ảnh Của Đường Tròn Qua Phép Tịnh Tiến: Phương Pháp Hình Học
Ngoài phương pháp đại số, ta cũng có thể sử dụng phương pháp hình học để tìm ảnh của đường tròn. Phương pháp này dựa trên tính chất của phép tịnh tiến.
-
Xác định tâm I của đường tròn ban đầu.
-
Tìm ảnh I’ của tâm I qua phép tịnh tiến theo vectơ v.
-
Vẽ đường tròn (C’) có tâm I’ và bán kính bằng bán kính của đường tròn ban đầu. Đường tròn (C’) chính là ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ v. Cùng xem truc tuyen today để cập nhật thêm nhiều kiến thức bổ ích.
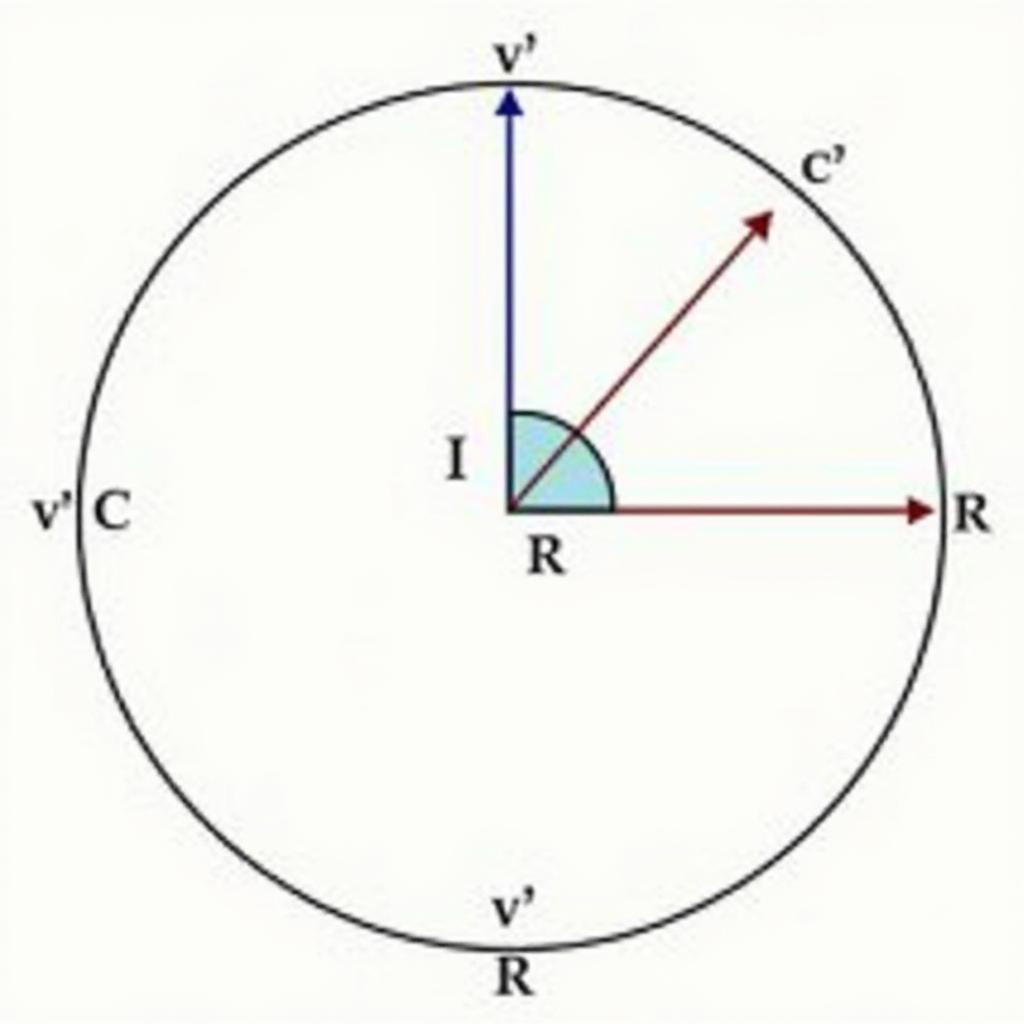 Minh họa phương pháp hình học tìm ảnh đường tròn qua phép tịnh tiến
Minh họa phương pháp hình học tìm ảnh đường tròn qua phép tịnh tiến
Ví Dụ Minh Họa
Cho đường tròn (C): (x – 1)² + (y – 2)² = 4 và vectơ tịnh tiến v(3, 1). Tìm ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ v.
Giải:
Tâm I(1, 2), bán kính R = 2.
Tâm I’ của đường tròn ảnh: I'(1+3, 2+1) = I'(4, 3).
Phương trình đường tròn ảnh (C’): (x – 4)² + (y – 3)² = 4. Đọc thêm về u20 han quoc để thư giãn sau bài toán này.
Kết luận
Tìm ảnh của đường tròn qua phép tịnh tiến là một dạng bài toán cơ bản trong hình học. Bài viết đã trình bày hai phương pháp chính để giải quyết bài toán này: phương pháp đại số và phương pháp hình học. Hy vọng bài viết đã cung cấp cho bạn những kiến thức hữu ích về “tìm ảnh của đường tròn qua phép tịnh tiến”.
FAQ
- Phép tịnh tiến là gì?
- Làm thế nào để tìm ảnh của một điểm qua phép tịnh tiến?
- Phương trình đường tròn là gì?
- Vectơ tịnh tiến là gì?
- Tại sao bán kính của đường tròn ảnh không thay đổi sau phép tịnh tiến?
- Có những phương pháp nào để tìm ảnh của đường tròn qua phép tịnh tiến?
- Ứng dụng của phép tịnh tiến trong thực tế là gì?
Bạn có thể xem bong da tren vtv6 hoặc tìm hiểu cách giải bài toán sau.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 0372999996, Email: [email protected] Hoặc đến địa chỉ: 236 Cầu Giấy, Hà Nội. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.